蓝桥云课 Problem.176 螺旋折线

发布于 2024-03-09  271 次阅读

原链: https://www.lanqiao.cn/problems/176/learning/

一、原题

（1）题目描述

如下图所示的螺旋折线经过平面上所有整点恰好一次

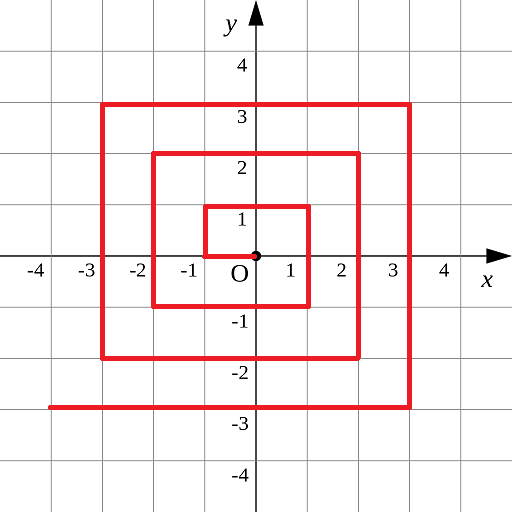
对于整点 （X， Y），我们定义它到原点的距离 dis（X ， Y）是从原点到 （X， Y）的螺旋折线段的长度。
例如 dis（0，1）= 3，dis（-2，-1）= 9
给出整点坐标（X，Y），你能计算出 dis（X，Y）吗？

（2）输入描述

输入格式：
输入一行，X 和 Y，-109 ≤ X，Y ≤ 109

（3）输出描述

输出 dis（X，Y）

（4）样例

输入

0 1

输出

3

二、思路

观察题目所给的图片可知，该螺纹每次发生长度变化的点位均在 y = - x 的函数上

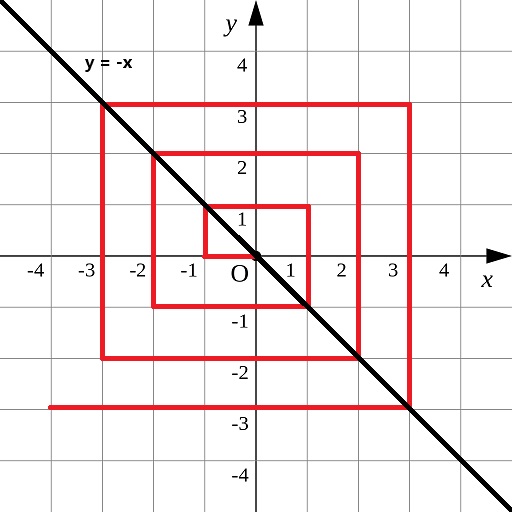
整理 y = - x 函数上的点到原点的螺纹折线段的长度，并进行推理
可以得出，对于 y = - x 函数上的点到原点折线段的长度

x ＞ 0f(x) = 4x2 + 2x
x ＜ 0f(x) = 4x2 - 2x
x = 0f(x) = 0

再次观察题目所给的图表，我们可以发现整个螺旋纹被我们前面观察出来的 y = -x 函数分割成两个部分
因为我们已经确定 y = -x 函数上的点是两个螺旋折线段的分界点，因此
当点 （x，y） 在函数上方时，意味着其分界点的下一个螺纹上，需要加上 x 和 y 作为偏移量，反之亦然

三、代码

import java.util.*;
public class Problem176 {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        long x = in.nextLong();
        long y = in.nextLong();
        System.out.println(dis(x, y));
    }

    public static long dis(long x, long y) {
        // 注意数字大小应该是long，int会超限
        long n = (int) Math.max(Math.abs(x), Math.abs(y));
        // 判断点是在 y = -x 函数的上边还是下边
        // y = -x 函数上的点都是一个螺纹的分界点
        if (x == -n || y == n)
            // 当点在上边时
            // 点 (x, y) 在分界点的下一个螺纹上，需要加上 x 和 y 作为偏移量
            return (long) (n * (n * 4L - 2) + x + y);
        else if (x == n || y == -n)
            // 当点在下边时
            // 点 (x, y) 在分界点的上一个螺纹上， 需要减去 x 和 y 作为偏移量
            return (long) (n * (n * 4L + 2) - x - y);
        
        // 无作用，Java编译器强制要求
        return 0;
    }
}